Динамика воблера

О изготовлении и тестировании воблера см. по ссылке:/publ/82-1-0-1139

Когда публикуются статьи о самодельных воблерах, в них, как правило, самым тщательным образом описываются методики, используемые в работе. Статьи подробно и, я бы даже сказал, дотошно рассказывают о том, как надо делать, но совершенно не объясняют, что надо делать. Проще говоря, в статьях отсутствует самое главное, а именно – как конструкция приманки влияет на её игру. Не могу сказать, что я являюсь крупным «докой» в данном вопросе, но, после нескольких консультаций у специалистов, у меня, наконец-то, сложилась более-менее цельная картина гидродинамики воблера. Пользуясь представившейся возможностью и чувствуя необходимость освещения этой относительно мало изученной проблемы, я и хочу предложить на суд читателя небольшое изложение основных физических принципов работы воблера и факторов, влияющих на его работу.

Что такое воблер, наверное, известно, если не всем рыболовам, то каждому спиннингисту уж точно. Похожие и не похожие на рыбу, большие и маленькие, яркие и невзрачные, стройными рядами лежат они на прилавках любого рыболовного магазина, все их видели. Вот устройство этой приманки детально известно не всем, ведь дополнительная огрузка, погремушки, система дальнего заброса – всё это, как правило, скрыто под слоем краски. А почему он, воблер, вообще работает, задумываются немногие. В первую очередь, те, кто сам пытается их делать.

Данная статья ориентирована, прежде всего, на рыболовов, которые собираются заняться изготовлением воблеров. Но и остальным, я надеюсь, будет достаточно интересна.

Немного физики

Тех, кому ещё в школе надоел предмет, указанный в подзаголовке, прошу заранее не пугаться: физики во всём страшном великолепии её «трёхэтажных» формул не будет. Практическая гидродинамика – дисциплина достаточно сложная, до конца понятная только специалистам, и я к ним не принадлежу. Так что все последующие рассуждения носят чисто умозрительный характер, хотя и с некоторой претензией на научную основу. Я заранее прошу прощения у тех специалистов, которым на глаза попадётся данная статья, за неточности и возможные ошибки. И буду очень признателен, если меня поправят.

Впрочем, те, кому мои рассуждения не очень интересны, могут просто пропустить их и перейти сразу к расположенным после них выводам. Но тогда последние просто придётся принять на веру.

Итак, что собой представляет воблер? Это некое тело более-менее обтекаемой формы, которое вряд ли смогло бы вилять из стороны в сторону, а тем более вибрировать, если бы не некий дестабилизирующий элемент. Обычно это наклонная поперечная пластина (лопасть), выступающая из передней части приманки, реже плоский косой срез самой передней части. Упомянутый элемент и заставляет обтекаемое тело совершать рыскающие колебания в набегающем потоке воды, а также погружаться при движении за счёт наклона к продольной оси воблера. Для понимания динамики этого процесса и влияющих на неё факторов рассмотрим схему сил, действующих на воблер.

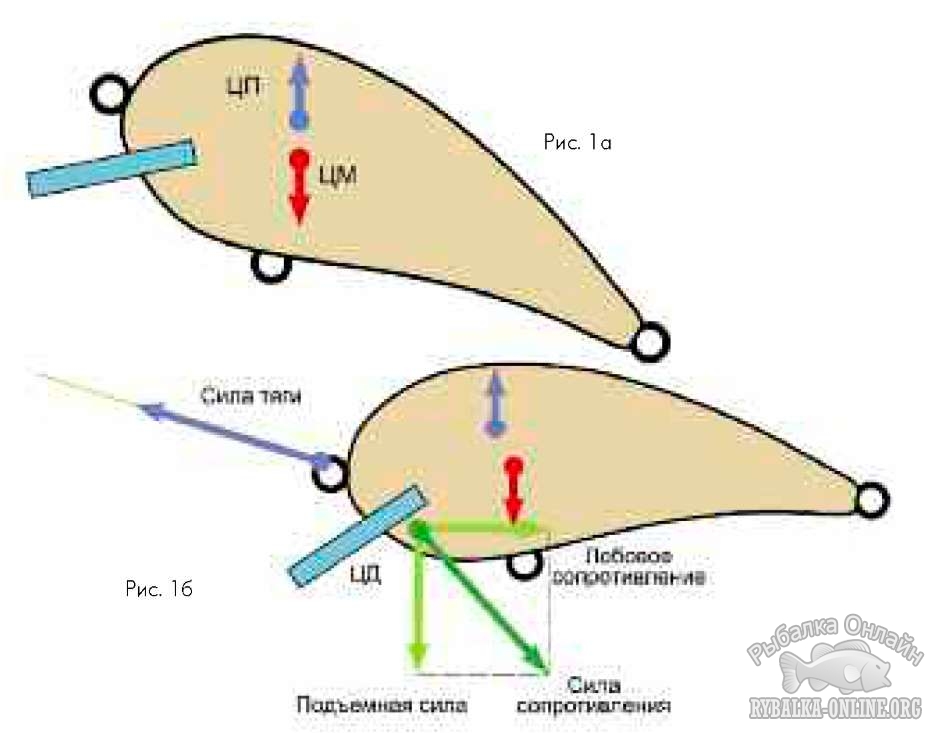На неподвижный воблер действуют только сила тяжести и сила Архимеда. Точкой приложения первой из них, направленной вертикально вниз, является центр масс (центр тяжести) тела. Вторая же, направленная вверх, приложена к так называемому центру плавучести – условной точке, которая являлась бы центром масс воблера, если бы он имел одинаковую плотность по всему объёму (в том числе лопасть, арматура, тройники и т.д.). Указанные две силы разворачивают находящийся в толще воды воблер в такое положение, чтобы центр плавучести находился чётко над центром тяжести (рис. 1а). Чем больше расстояние между центрами, тем быстрее воблер приходит в это положение, тем лучше его остойчивость. Если плавучесть положительна (т.е. сила Архимеда больше силы тяжести), погружённое в жидкость тело стремиться всплыть, а если она отрицательна, то погрузиться.

На воблер в движении действуют ещё и сила натяжения лески, а попросту сила тяги, приложенная к передней петле, а также противодействующая ей сила сопротивления воды. Точку приложения этой силы будем называть центром давления (рис. 1б). Процедура определения точного местоположения этого центра достаточно сложна и неосуществима в домашних условиях, локализовать его можно лишь приблизительно, пользуясь простыми рассуждениями. Само по себе тело воблера, как уже говорилось, имеет обтекаемую форму, и его собственная сила сопротивления сравнительно невелика. А вот дестабилизирующий элемент обладает гидродинамически невыгодной формой и, несмотря на сравнительно незначительные размеры, оказывает довольно сильное сопротивление потоку. Поэтому следует ожидать, что центр давления всей приманки будет локализован где-то ближе к лопасти (срезу). Всё, конечно, зависит от размеров и формы лопасти и собственно тела воблера. Ещё следует заметить, что положение центра давления зависит от ориентации воблера к направлению потока, но мы пока предположим, что оно не меняется.

Силу сопротивления традиционно раскладывают на две составляющие – силу лобового сопротивления, параллельную направлению набегающего потока, и перпендикулярную ей, которую по традиции называют подъёмной силой. Последняя, несмотря на название, не обязательно направлена вертикально вверх. Она может быть направлена вниз, как в нашем случае, или даже вбок.

Будем предполагать, что воблер симметричен относительно вертикальной плоскости. Тогда, по логике, центр давления воблера в равновесном положении лежит в этой плоскости, как и центры масс и плавучести, а также передняя петля, т.е. точки приложения всех сил, действующих на приманку. И векторы сил тоже лежат в этой плоскости.

Поступательное движение воблера

Сначала давайте разберёмся, как и почему воблер ныряет. Для этого, так сказать, запретим воблеру колебаться и жёстко зафиксируем его в плоскости симметрии. То есть, если воспользоваться авиационной терминологией, пусть изменяется только угол тангажа (наклон вперёд или назад), а углы рыскания (поворот влево-вправо вокруг вертикальной оси) и крена (наклон влево-вправо) будут постоянны и равны нулю. Также предположим, что влияние силы тяжести и силы Архимеда ничтожно малы (т.е. натяжение лески и сопротивление жидкости намного больше), а центр давления при изменении угла тангажа никуда не смещается.

Что же произойдёт, если потянуть за леску? Понятно, что чем больше её натяжение, тем больше и сила сопротивления. Но точки приложения у них разные, да и векторы их не всегда разнонаправлены, а в общем случае образуют тупой угол. Возникает вращающий момент, заставляющий воблер опускать нос до тех пор, пока центр давления не окажется на линии натяжения лески (рис. 1в), при этом приманка двигается не в направлении потяжки, а вперёд и одновременно вниз. Чем меньше угол наклона лопасти к продольной оси воблера, тем меньше лобовое сопротивление и больше подъёмная сила. Соответственно, воблер заглубляется быстрее.

Если приманка движется с постоянной скоростью, значит, силы тяги и сопротивления компенсируют друг друга. То есть они равны по значению, а их и векторы противоположно направлены (см. рис. 1в). Угол α₀ между любым из этих векторов и направлением движения воблера – величина постоянная, не зависящая от скорости (специалистам, которые сразу вспомнили о числе Рейнольдса, напоминаю: все наши рассуждения носят достаточно приближённый характер, тем более что сказанное достаточно хорошо выполняется в широком диапазоне скоростей). По мере заглубления воблера направление вектора силы тяги меняется, и когда его угол к горизонтали становится равным α₀ (рис. 1г), приманка достигает своей рабочей (максимальной) глубины. Эта глубина определяется только длиной лески и тоже не зависит от скорости движения. Если, конечно, не учитывать влияние сил Архимеда и тяжести. Тонущий воблер будет идти чуть глубже, а плавающий – немного ближе к поверхности, чем суспендер. И чем меньше скорость проводки, тем существеннее это различие.

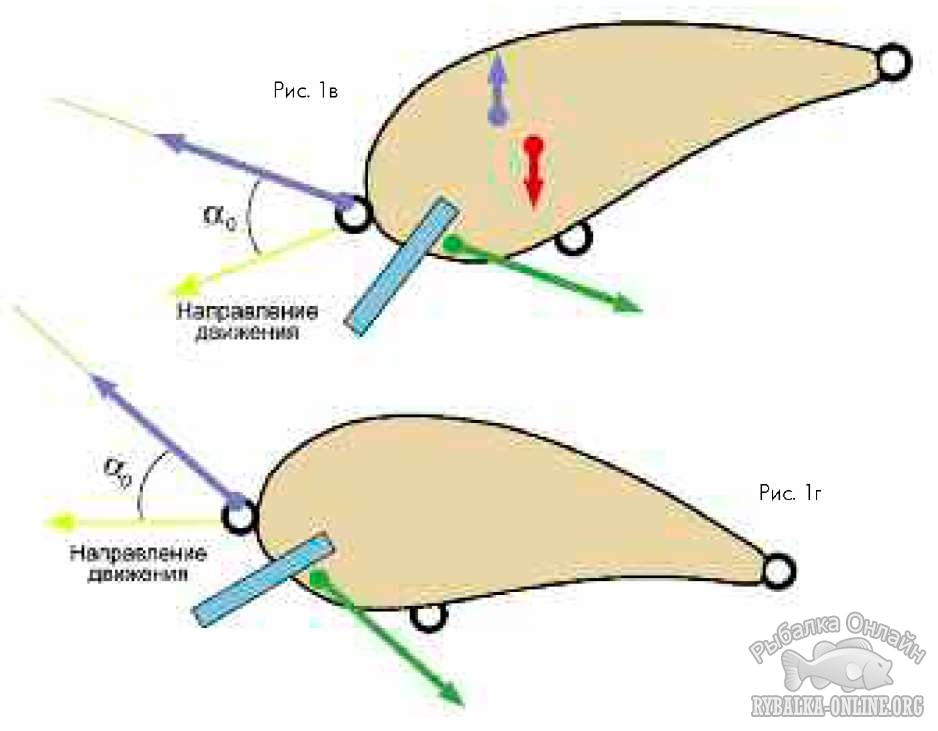
Если длина лески l постоянна (например, воблер тянется за движущейся лодкой), тогда расчётная глубина хода будет равна lsinα₀ (надводную часть лески мы не здесь учитываем). Впрочем, нагляднее будет рассматривать зависимость глубины не от l, а от горизонтального расстояния x до приманки. Тогда расчётная глубина равна xtgα₀. На самом деле, конечно, эти рассуждения весьма условны и справедливы лишь при небольших значениях l или x, поскольку не учитывают собственного сопротивления лески набегающему потоку, в результате которого её выгибает дугой и реальное заглубление приманки получается меньше расчётного. При больших x, когда леска на ближайших к рыболову метрах почти параллельна поверхности воды, глубина хода воблера становится практически постоянной. Это значение y₀ и понимают под термином «рабочая глубина» (надо сказать, что y₀ зависит и от диаметра лески: у более тонкой сопротивление потоку меньше, соответственно её меньше выгибает, и воблер движется глубже). Выражаясь математически, можно сказать, что кривая зависимости глубины хода от горизонтального расстояния y = f(x) имеет две асимптоты:
y = xtgα₀ при x > 0 и y = y₀ при x > ∞ (рис. 2) .

Если же спиннингист крутит ручку катушки, то длина лески всё время уменьшается, как и её угол к поверхности воды. В то же время угол между силой тяги и направлением движения α₀ не изменяется.

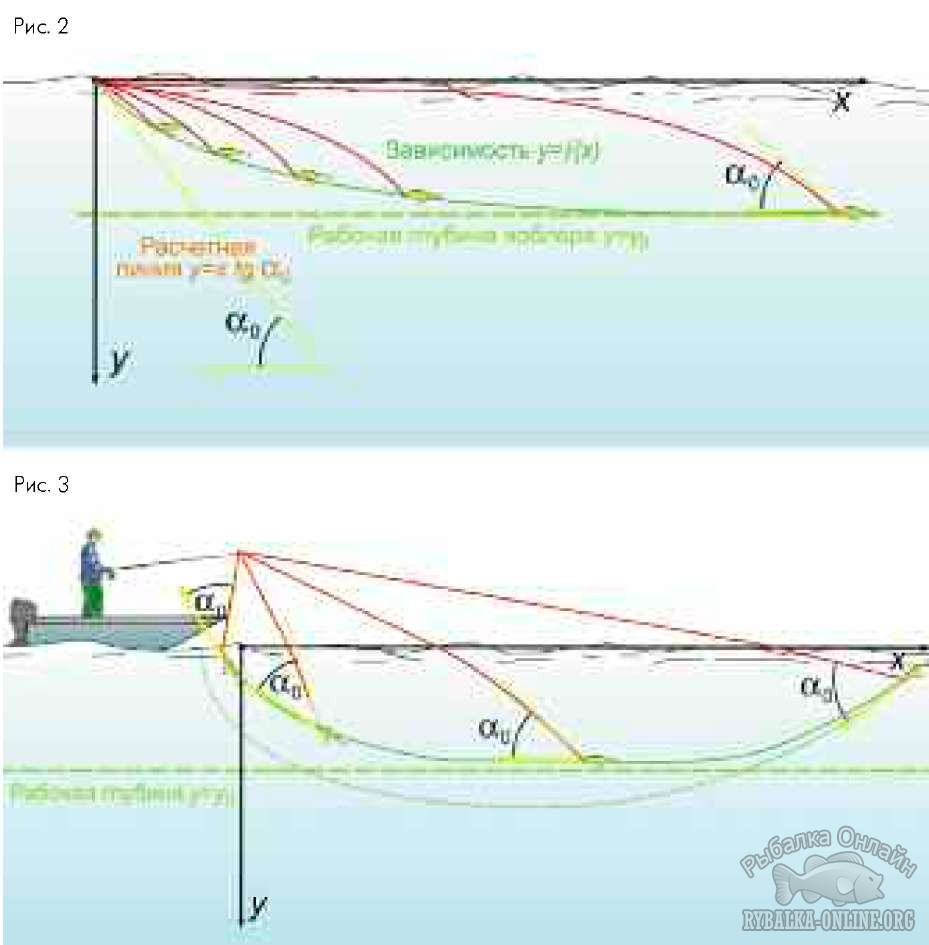Расчёт траектории движения приманки в воде даёт дугу с плавно уменьшающимся радиусом – сходящуюся спираль, которая закручивается вокруг начала координат, связанного с кончиком спиннинга (специально для любителей математики привожу результаты расчётов: траектория как зависимость глубины от горизонтального расстояния x задаётся параметрически с помощью системы уравнений {x = lcosφ; y = lsinφ - l₀sinφ₀}, где полярный угол φ выражается через параметр l (длину лески) формулой φ = φ₀ - tgα₀ ln(l/l₀). Здесь l₀ – длина лески в начале движения (максимальная длина лески), а φ₀ – начальное значение полярного угла при l = l₀ (при глубине y = 0)); примерно такую форму имеет часовая пружина. Однако область применения и этих вычислений весьма ограничена. Они работают только на небольших дальностях заброса (малых l₀), когда сопротивление лески в воде намного меньше собственного сопротивления воблера. Когда влияние лески существенно, реальная траектория проходит выше по глубине. На полной дальности заброса воблер сначала достаточно резко погружается, быстро достигает максимальной глубины (которая примерно равна рабочей) и постепенно приближается к поверхности по мере выматывания лески, а в конце движения резко поднимается (рис. 3). 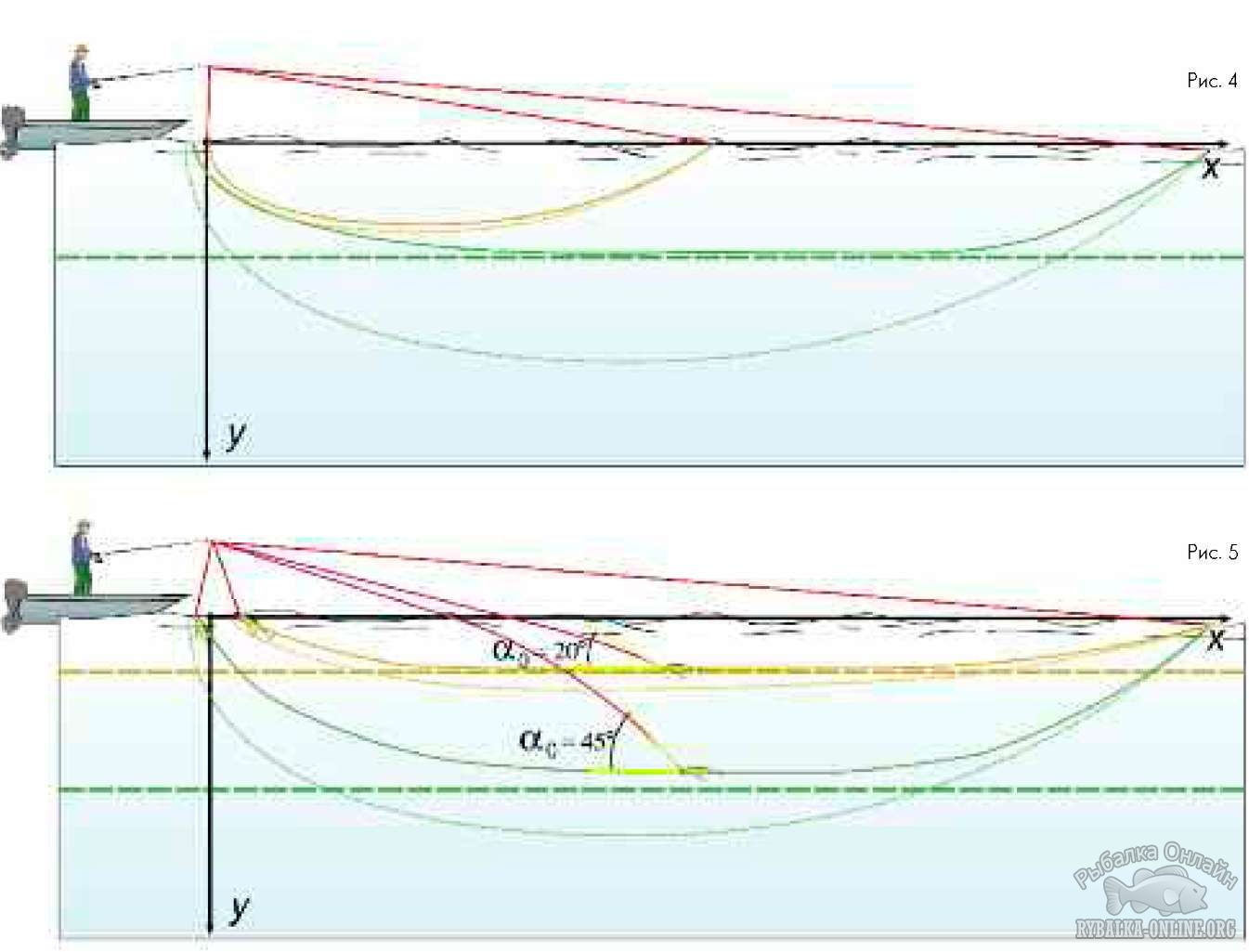Чем дальше заброс, тем больше заглубление воблера приближается к его рабочей глубине и тем больше времени проводит приманка на данной глубине (рис. 4). Чем ниже угол α₀, тем меньше воблер заглубляется. Соответственно, сопротивление лески оказывает меньшее влияние на заглубление, а реальная траектория больше похожа на расчётную, особенно на малых дальностях заброса (рис. 5).

Примечательно, что дальность хода воблера со значительной глубиной хода (большим α₀) может превышать дальность заброса: точка выхода приманки на поверхность по горизонтали будет находиться ближе к рыболову, чем кончик спиннинга. Кроме того, при определённых условиях приманка в конце траектории даже может двигаться в противоположную от спиннингиста сторону. Впрочем, эти особенности присущи только приманкам с большим заглублением и не имеют практического значения в рыбалке. Они проявляются лишь тогда, когда тюльпан спиннинга опущен близко к поверхности воды, и представляют скорее неудобство: можно провести приманку слишком близко к себе и зацепить крючком о днище лодки, с которой производится ловля.

Надо сказать, что и рассуждения, учитывающие выгибания подводной части лески под действием набегающего потока, тоже не вполне точны, поскольку не учитывают прогиб её надводной части вниз под действием силы тяжести. За счёт этого «подводные эффекты» лески становятся заметны на меньших расстояниях l.

Сложно? На самом деле всё ещё сложнее, поскольку при любых эволюциях воблера относительно набегающего потока меняется и положение центра давления, и сила сопротивления, что тоже необходимо учитывать. Но для понимания пока сойдёт и так.

До сих пор мы предполагали, что воблер идеально сбалансирован и векторы сил тяги и сопротивления находятся на одной линии, как показано на рис. 6а. А что будет, если эти векторы не лежат в одной плоскости? Такое случается, если лопасть асимметрична или перекошена в одну сторону (впрочем, возможно и то и другое вместе). 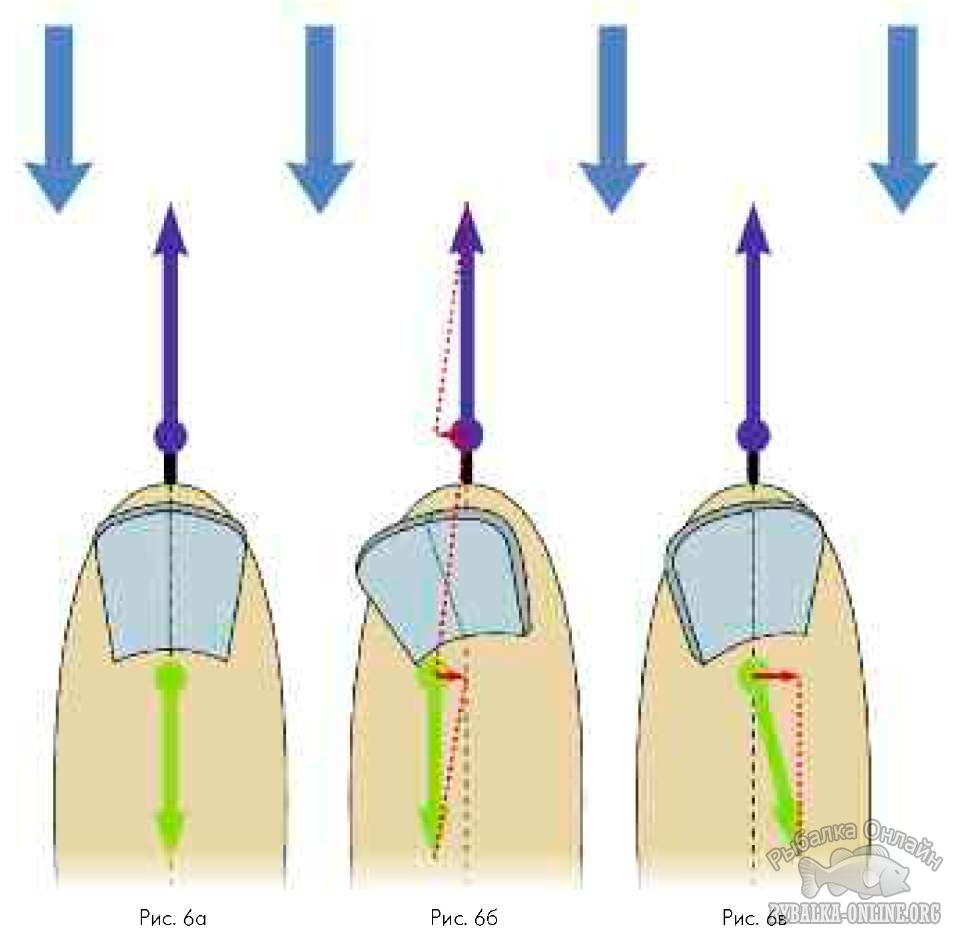Оба эти случая проиллюстрированы на рис. 6б и 6в. Ситуации разные, но результат одинаков: возникает вращательный момент, заставляющий воблер поворачиваться вбок и (мы помним, что точка приложения силы тяги находится выше точки приложения силы сопротивления, т.е. центра давления) одновременно крениться в противоположную сторону. В случае, изображённом на рисунке, воблер начинает смещаться влево по ходу движения и при этом кренится на правый бок. Момент сил тяжести и Архимеда, который тем больше, чем сильнее крен, старается, наоборот, выровнять воблер. При некотором угле крена моменты сил могут уравновеситься, и приманка будет двигаться вперёд с креном в одну сторону и отклонением от курса в другую. Если же скорость движения достаточно высокая, так что отклоняющий момент всегда больше выравнивающего, воблер будет двигаться по спирали, пока его не вынесет на поверхность. Как этого избежать? Необходимо сместить вбок одну из точек приложения сил – либо силы тяги (подогнуть переднюю петлю в сторону крена воблера), либо центра давления (сточить лопасть с этой стороны).

Механизм колебаний воблера

Теперь проанализируем причину собственно игры воблера. Сначала допустим, что воблер уже находится на рабочей глубине (подъемная сила уравновешена вертикальной компонентой силы тяги), при этом угол вектора силы тяги к вертикали не меняется. Смоделировать эту ситуацию просто: представьте, что ручка спиннинговой катушки не крутится, а приманка заглублена и колеблется лишь под действием течения. Другой пример: троллинг с постоянной скоростью. Еще предположим, что влияние пары вертикальных сил (Архимеда и тяжести) мало по сравнению с гидродинамическими силами, что реализуется на сильном течении (или при большой скорости лодки). В этом случае поведение приманки определяется преимущественно силами тяги и сопротивления. Однако следует помнить, что колебания происходят, в основном, вокруг вертикальной оси, поэтому совсем сбрасывать со счетов вертикальные силы нельзя: некоторую роль они, безусловно, играют. Ну, и, наконец, для простоты будем предполагать, что турбулентность мала.

Как известно, если в механической системе происходят колебания, значит, должна быть отклоняющая сила и сила, возвращающая систему в положение равновесия. Логично будет предположить, что отклоняющую силу у воблера создает именно пластина, расположенная в его носовой части, а возвратная сила связана собственно с обтекаемым телом, стремящимся развернуться в направлении навстречу потоку. Но с силами мы, допустим, разобрались, а вот с механизмом колебаний не все так просто. Попытка рассмотреть игру приманки поэтапно встречает определенные затруднения. Лично для меня модель колебаний окончательно оформилась уже после обстоятельной беседы со специалистом. Сейчас я и попытаюсь изложить эту модель. Здесь вместо общего сопротивления приманки будет уместно рассмотреть отдельно силы сопротивления лопасти и тела, каждую со своим центром давления (ЦД). Для простоты пока что будем считать, что диметр лески бесконечно мал (т.е. сопротивление воде ничтожно), а длина достаточно большая, чтобы можно было считать леску параллельной направлению набегающего потока.

Пусть в начальный момент времени плоскость симметрии приманки вертикальна и параллельна направлению набегающего потока (рис. 7а). Если рассматривать только рыскание воблера, т. е. повороты вокруг вертикальной оси, то такое положение приманки устойчиво: при любом смещении влево-вправо возникают поперечные силы, старающиеся вернуть ее в исходное положение (рис. 7а'). Колебания возможны, только если вначале принудительно развернуть воблер вбок и отпустить. Более того, эти колебания будут быстро затухающими, поскольку вода - среда вязкая, обладающая значительными демпфирующими (гасящими) свойствами. Попробуйте запустить маятник, окунув его в воду, и вы все поймете. К чему я это веду? К тому, что в устойчивую амплитуду, а тем более возрастающую на начальном этапе, верится слабо, если рассматривать только рыскающие колебания вокруг вертикальной оси.

Иное дело, если допустить возможность синхронных с ними колебаний вокруг продольной оси (крен). Если присмотреться к работе любого воблера, можно заметить, что помимо отклонений влево-вправо во время игры, он еще и кренится в разные стороны. Эти колебания происходят с той же частотой, что и вертикальные, но опережают их по фазе примерно на величину п/2, а по времени, соответственно, на четверть периода. У одних воблеров они более заметны, у других - менее, у третьих вообще практически незаметны, но они есть. Именно взаимодействие этих двух колебаний и создает устойчивую игру воблера. Как это происходит, мы сейчас рассмотрим по несколько упрощенной схеме, поэтапно.

Итак, в начальный момент времени воблер находится относительно потока в положении равновесия, изображенном на рис. 7а. Вертикальную плоскость, которая в данный момент совпадает с обозначенной пунктиром плоскостью симметрии воблера, будем называть нулевой. На приманку, в противоположность направленной вперед и вверх силе тяги, которая приложена к передней петле, действуют силы сопротивления лопасти и тела, приложенные к своим центрам давления. Первая направлена назад и вниз, вторую будем считать чисто горизонтальной. По логике, первая должна быть существенно больше второй, таковы условия обтекания плоской пластины и обтекаемого тела. Также полагаем, что центры давления никуда не смещаются при эволюциях воблера, хотя это и не совсем так, особенно в отношении ЦД тела. В положении равновесия все три силы лежат в нулевой плоскости и компенсируют друг друга. Заметим, что ЦД лопасти находится ниже ЦД тела, это важно. Предположим, что вследствие, скажем, случайной турбулентности приманка чуть-чуть довернулась влево, как показано на рис. 7а'.

В таком положении, как уже было сказано, на приманку действуют поперечные силы, старающиеся развернуть ее обратно. Но их точки приложения находятся на разной высоте. Точки приложения силы тяги и силы сопротивления тела лежат в районе продольной оси воблера, эти силы разворачивают воблер вокруг вертикальной оси. А вот центр давления лопасти лежит ниже, и под действием силы сопротивления пластины приманка еще и проворачивается вокруг своей продольной оси (рис. 7б). Фактически реализуется состояние, проиллюстрированное на рис. 6в: скошенная вбок пластина заставляет воблер крениться и двигаться в сторону.

По мере разворота воблера в исходное положение боковые составляющие двух первых сил уменьшаются. А вот поперечная составляющая сопротивления лопасти может даже увеличиваться за счет крена. Ключ в том, что даже в продольном положении приманки, когда боковые составляющие тяги и сопротивления тела равны нулю (рис. 7в), сопротивление лопасти продолжает разворачивать воблер, отклоняя его уже вправо. Но такое положение воблера, по сути, это ситуация, изображенная на рис. 6б, когда лопасть смещена вбок. И продолжая отклоняться вправо под действием боковых сил, а также инерции, приманка будет стремиться накрениться в противоположную сторону и довольно быстро снова займет вертикальное положение (рис. 7г). А это, как видим, почти та же ситуация, что и на рис. 7а', только зеркально симметричная. Снова происходит крен и разворот приманки в противоположную сторону - начинается второй полупериод колебаний (рис. 7д).

Это, конечно же, упрощенная схема. На самом деле в динамике рассмотренные процессы происходят не один за другим, а накладываются друг на друга; возвращающие силы действуют одновременно с отклоняющими, просто на определенных этапах одни доминируют над другими. Но основной принцип, я думаю, понятен.

Как мы видим, задает колебания головная часть, в которой расположена пластина, а хвостовая часть (тело) отслеживает эти колебания с некоторым запаздыванием из-за своей инерции. Поэтому траектория воблера в воде представляет собой не просто прямолинейное движение с одновременными доворотами влево-вправо вокруг одной и той же оси, а некую "змейку". Это особенно хорошо заметно при наблюдении за игрой воблера, состоящего из двух или нескольких частей. Инерция тела при вращении вокруг вертикальной оси (поворотах) сильнее, чем при вращении вокруг продольной оси (наклонах), именно поэтому колебания устойчивы, а на начальном этапе их амплитуда может возрастать.

Наклоняясь на бок, воблер вынужден всякий раз преодолевать выравнивающее действие сил Архимеда и тяжести, стремящихся вернуть его в вертикальное положение. На больших скоростях их влияние на игру практически нивелируется, поскольку

гидродинамические силы значительно превышают их по величине. Но вертикальные силы имеют большое значение в плане стабилизации игры. На критических скоростях уровень турбулентности может быть таким, что нарушается симметрия обтекания приманки, в результате чего ее ЦД может сместиться вбок. Понятно, что в этом случае воблер, даже идеально отрегулированный, начнет заваливаться на бок, причем нельзя заранее сказать, в какую сторону. Выглядит это так: не прекращая играть, приманка бросается то в одну, то в другую сторону, а при дальнейшем увеличении скорости окончательно заваливается на один бок и двигается к поверхности, как плохо отрегулированная. Так вот, вертикальные силы оказывают выравнивающее действие, повышая критическую скорость и сдвигая рабочий диапазон скоростей приманки в сторону больших значений, что очень важно, например, при ловле на течении. Поэтому, как правило, стараются усилить действие этих сил, вертикально разнося центр тяжести и центр плавучести приманки (увеличивая остойчивость) с помощью дополнительной огрузки. Однако на малых скоростях, когда гидродинамические силы невелики, наши вертикальные силы могут составить им серьезную конкуренцию, уменьшая крен приманки и, как следствие, колебаний игры. Иногда даже могут появиться некоторые проблемы с возникновением этих колебаний.

Чтобы колебания запустились, нужно некое начальное отклонения воблера от положения равновесия - либо вертикальное (рис. 7в), либо горизонтальное (рис. 7а'). Последнее часто случается, когда после заброса в момент начала подмотки приманка находится под углом к леске. Если же воблер с леской на одной линии, то, как уже говорилось, начальное отклонение может произойти вследствие турбулентности, причем иногда для этого требуется довольно значительная скорость. Опытные спиннингисты наверняка сталкивались с воблерами, которые можно заставить играть, лишь разогнав до некоторой пороговой скорости (причем при последующем снижении скорости колебания уже не пропадают, просто снижается амплитуда). Особенно часто этим грешат классические твитчбейты, которые создаются специально для работы на сравнительно больших скоростях во время рывковой проводки. Они, как правило, оснащены небольшой лопастью и обладают сравнительно малоамплитудной игрой. Но в данной статье мы больше внимания уделим так называемым крэнкбейтам - воблерам со сравнительно большой амплитудой колебаний. А уж как ее уменьшить, способ всегда найдется.

Кстати, об амплитуде и частоте. Важно отметить, что, увеличивая тем или иным способом амплитуду колебаний (а она определяет интенсивность акустических волн, испускаемых приманкой), мы обычно жертвуем частотой. И наоборот, большая частота вибрации приманки чаще всего соседствует с малой амплитудой. Ниже я попытаюсь описать, как конструктивные особенности приманки определяют эти параметры, но сначала хотел бы вернуться к вопросу о влиянии лески на игру.

Напомню, мы предполагали, что леска бесконечно тонкая и на игру воблера воздействия не оказывает. На самом деле это, конечно, не так. Леска имеет собственное сопротивление потоку, что проявляется и при боковых перемещениях. Подобно случаю, изображенному на рис. 2, поток и в горизонтальной плоскости дугой выгибает леску, вследствие чего последняя сообщает воблеру дополнительную возвращающую силу (рис. 8). И чем толще леска, тем круче дуга и тем больше данная сила. Она препятствует отклонению воблера, уменьшая амплитуду, и быстрее возвращает его в исходное положение, увеличивая частоту колебаний. А достаточно толстая леска не только нарушает игру воблера, она может стать причиной полного прекращения колебаний. Поэтому некоторые производители в характеристиках воблеров указывают оптимальную для них толщину лески.

И что с этим всем делать?

Теперь проанализируем влияние конфигурации воблера на его игру. Сначала немного о форме тела. Как уже упоминалось, ей обычно придают, по возможности, максимальную обтекаемость, чтобы лобовое сопротивление собственно тела было минимальным. Нужно учитывать, что воблеры обычно работают с дифферентом на нос, особенно те, у которых лопасть расположена под небольшим углом к потоку. Поэтому оптимальным будет сечение яйцевидной формы, широкой частью вверх. Такое сечение удобно еще по одной причине.

Центр плавучести тела будет выше средней линии, а центр масс существенно сместится книзу за счет массы арматуры, крепящей ее эпоксидной смолы, лопасти и тройников, а также дополнительной огрузки, если такая есть. Чем больше расстояние между этими центрами, тем выше остойчивость воблера, тем больше скорости, на которых он сможет устойчиво работать.

Тело создает также сопротивление боковой поверхностью во время колебаний, при смещениях влево-вправо. С этой точки зрения лучше подходит круглое сечение. Оно наиболее экономично, если дифферент на нос небольшой, что характерно для воблеров с длинным и тонким профилем тела или с лопастью, установленной под большим углом к потоку. Круглое сечение даст хорошую амплитуду колебаний, хотя здесь мы теряем в остойчивости, поэтому такие воблеры желательно доогружать. Другой его недостаток - большая площадь по сравнению со сплюснутым с боков, что, как мы уже обсуждали, тоже ведет к снижению критической скорости и уменьшению рабочего диапазона скоростей в целом. Впрочем, круглым сечение можно сделать не по всей длине тела, а только в хвостовой части, где боковая скорость во время колебаний наибольшая.

И о профиле тела, по которым, собственно воблеры и различают. Их существует великое множество. И, как обычно, возможны две крайности. С одной стороны, есть длинные и тонкие приманки, которые принято называть "minnow", поскольку по форме они напоминают малька. В противоположность им есть воблеры с коротким телом сравнительно большой толщины. Они, как правило, менее стабильны на больших скоростях и больше подвержены заваливанию вбок при увеличении скорости (во всяком случае, сделать стабильный "минноу" заметно проще). Но именно эти воблеры и являются классическими крэнкбейтами, поскольку лучше сохраняют высокую частоту при относительно большой амплитуде колебаний, чем длинные "минноу", так как последние более инерционны (фото 1).

А если нужно сделать длинный воблер, обладающий одновременно высокой частотой и амплитудой? Оригинальное решение в свое время предложил Лаури Рапала, легендарный финн, давший миру воблер классической схемы. Он придумал... распилить воблер на части, оснастив подвижным соединительным коленом. Так получился составной воблер (фото 2). Обо всех его достоинствах я здесь рассказывать не буду, это тема отдельной статьи. Скажу только, что нужным образом сбалансированный составник является высокочастотным крэнкбейтом, несмотря на свои иногда довольно значительные размеры. Ведь колебания задает только сравнительно короткая передняя часть, оснащенная лопастью, а задняя часть или части повторяют ее движения. Инерционность всего составника определяется, в основном, инерционностью его передней, рабочей части.

Согласно принципам динамики вращательного движения (а у нас колебания именно такого типа), инерция тела при вращении (т. е. его сопротивляемость раскрутке и торможению) зависит не только от его массы, но и от ее распределения по телу. Чем дальше элемент массы от оси вращения, тем инерционнее тело, тем труднее ее раскрутить и затормозить. Здесь самое время еще раз сказать об огрузке воблера.

Помимо увеличения остойчивости, огрузка тела воблера имеет еще одно немаловажное значение: ее распределение влияет на амплитуду и частоту колебаний. Причем это влияние не всегда однозначно и зависит от других факторов. Общее правило таково: инерционность тела положительно влияет на амплитуду, уменьшая при этом частоту. Поэтому для увеличения амплитуды дополнительная огрузка должна располагаться подальше от мгновенной оси вращения тела воблера. Для классических крэнкбейтов - воблеров с коротким и толстым телом - целесообразно для этого огружать хвост, поскольку у них ось вращения сдвинута к передней части. У воблеров типа "минноу" она расположена ближе к центру, поэтому эффективной бывает и огрузка носа. Тем более в последнем случае дополнительный груз уравновешивает вес заднего тройника, и воблер при остановке движения располагается в толще воды горизонтально, напоминая внезапно остановившуюся рыбку. Это очень полезное свойство, например, для твитчбейта с нулевой плавучестью (суспендера).

С другой стороны, балансировка воблера важна не только при его движении в воде, немаловажную роль она играет и при забросе, что тоже нужно учитывать. Скажем, если центр масс расположен ближе к хвосту, то воблер, например, дальше летит. И, что еще более существенно, практически никогда во время заброса не происходит зацепа тройником за леску. Если огрузка в носовой части, то такие неприятные моменты все же случаются. При троллинге, когда приманка почти все время в воде, это не так существенно, а вот при ловле взаброс неудачно огруженным воблером частые зацепы за леску могут сильно испортить настроение.

Я умышленно не обсуждаю здесь тему плавучести воблеров, к которой огрузка имеет самое прямое отношение. Подбирайте место огрузки и ее величину экспериментально - это самый надежный способ добиться нужного эффекта. Скажу еще, что, помимо положительного значения - устойчивости воблера на больших скоростях, чрезмерная огрузка может иметь и отрицательное влияние: слишком устойчивый воблер плохо "заводится" и слабо играет на малых скоростях. Но это проявляется, в основном, у воблеров с ориентацией пластины, близкой к вертикальной.

И один нюанс, касающийся положения огрузки. На мой взгляд, огромным плюсом для той же рапаловской тонущей модели Countdown является то, что эта приманка играет даже во время свободного погружения, без участия рыболова или течения. Достигается это расположением огрузки в носу приманки, в результате чего сила тяжести работает как сила тяги. Точно так же можно заставить плавающий воблер совершать колебания и при свободном всплытии, если расположить огрузку в хвосте модели. Тогда воблер будет всплывать носом вверх, а в роли силы тяги будет сила Архимеда. Правда, достигнуть этого труднее, ведь такой воблер должен иметь хороший резерв плавучести, чтобы скорость всплытия была достаточной для возбуждения и поддержания колебаний.

Ну, а теперь о лопасти. Это, если разобраться, самый важный элемент данной приманки, который и делает воблер воблером. Я уже говорил, что лопасть должна создавать значительную часть сопротивления потоку. Из простых фигур именно у плоской пластины, поставленной перпендикулярно потоку, оно максимальное, а минимальное создает тело обтекаемой (каплевидной) формы. Для сравнения: плоская пластина круглой формы создает на порядок большее сопротивление, чем шар одинакового с ней диаметра, и на два порядка большее, чем тело обтекаемой формы того же максимального диаметра. Кстати, это широко используется в природе. Например, окунь - тело довольно-таки обтекаемой формы - способен, хорошо разогнавшись, практически мгновенно затормозить, просто растопырив сравнительно небольшие, но плоские плавники. Основная нагрузка при этом приходится, конечно, на грудные и брюшные, которые располагаются перпендикулярно (ну, или почти перпендикулярно) набегающему потоку.

Лопасть делают с расширением книзу, чтобы сместить вниз ее ЦД. Само собой, лопасть должна быть соразмерной с телом. Пластина со слишком малой площадью не даст для крэнкбейта достаточной амплитуды колебаний и необходимого заглубления, поскольку не будет иметь достаточного сопротивления и, соответственно, подъемной силы . Слишком большая будет создавать значительную турбулентность, что сделает игру неустойчивой. По опыту скажу, что лопасть не стоит делать шире тела воблера, а ее длина не должна сильно превышать высоту тела. Сказанное не касается так называемых ныряющих (diving) вобле-ров, оснащенных длинной широкой пластиной, расположенной под небольшим углом к продольной оси приманки, и передней петлей, вынесенной непосредственно на эту лопасть. Здесь я ничего советовать не стану, поскольку, честно говоря, до сих пор даже не попробовал сделать ныряющий воблер.

Насчет расположения лопасти можно сказать следующее. Ее ориентация по отношению к продольной оси воблера влияет не только на заглубление, но и частично на амплитуду колебаний, поскольку не так важен размер (площадь) лопасти, как ее видимый размер, если смотреть с направления движения воблера. Чем меньше угол пластины к продольной оси, тем меньше этот видимый размер и тем меньше эффективная площадь (рис. 9).

Еще раз повторюсь, что уменьшение угла пластины к продольной оси увеличивает рабочую глубину приманки. Но такой способ борьбы за увеличение глубины хода имеет один недостаток: при небольших углах установки лопасти уменьшается ее эффективная площадь и, соответственно, вклад в силу сопротивления, игра становится менее амплитудной. Приходится увеличивать размер пластины, что смещает общий центр давления приманки вперед. А чем он ближе к передней петле (точке приложения силы тяги), тем менее устойчивой становится игра приманки. Если же лопасть настолько крупная, что общий центр давления находится впереди петли, колебания вообще прекращаются, поскольку воблер, даже идеально отрегулированный, моментально ложится на бок. Приходится смещать переднюю петлю вперед, на саму пластину. Собственно говоря, так и возник ныряющий воблер.

Располагать плоскую лопасть под углом к оси, очень близким к прямому (например, для минимального заглубления), тоже не рекомендую: такая пластина не будет создавать достаточной подъемной силы. В результате приманка станет плохо работать на минимальных скоростях проводки, когда вертикальная пара сил (Архимеда и тяжести) еще имеет существенное влияние. Ну, по меньшей мере, воблер придется сначала разогнать до достаточно высокой скорости, чтобы "завести", т. е. запустить устойчивые колебания. Обратите внимание, что на серийных моделях, разработанных для небольших глубин, нижняя часть лопасти специально выгибается вперед. И даже на тонущих воблерах (например, рапаловский Countdown), способных опуститься на нужную глубину и без участия пластины, последняя тоже ставится под углом к оси, хоть и небольшим.

Место установки лопасти в теле воблера тоже имеет большое значение: оно определяет положение центра давления, а вследствие этого влияет на игру. На этот счет распространено мнение, что амплитуда тем больше, чем дальше расположена лопасть от передней петли (впрочем, в литературе иногда утверждается и обратное). Долгое время я принимал его на веру, пока не начал задумываться о природе колебаний воблера. Действительно, по теории выходит, что чем дальше друг от друга эти элементы, тем меньше амплитуда, как ни крути. Ведь чем больше расстояние между точками приложения сил тяги и сопротивления, тем больше возвращающий момент сил, возникающий при отклонении воблера (см. рис. 3д), тем легче (и раньше) воблер отклоняется назад, в сторону нулевой плоскости. В конце концов, я наскоро выточил тестовую заготовку воблера с четырьмя прорезями под лопасть на разных расстояниях от носа. Прорези выполнялись под одним и тем же углом к продольной оси тела. Чтобы центр масс заготовки не смещался при перестановке лопасти, заготовка вырезана из довольно тяжелого дерева, а сама пластина выполнена из очень тонкого плексигласа и почти ничего не весит. Прогнав тестовую модель в ванной, я убедился, что теория верна: при приближении лопасти к передней петле амплитуда колебаний возрастает (рис. 10). По-видимому, сторонники противоположного мнения приближали лопасть к передней петле, просто уменьшая угол ее установки к оси воблера. А это снижает силу сопротивления лопасти и сдвигает общий центр давления назад, что закономерно приводит к уменьшению амплитуды.

И в конце хочу сказать несколько слов о моделях и размерах. Казалось бы, увеличенная или уменьшенная копия рабочего воблера тоже должна хорошо играть и ловить рыбу. Однако не все так просто. Пытаясь повторить удачную модель в другом масштабе, будьте готовы к тому, что она не оправдает ваших ожиданий, будет неустойчивой или вообще откажется играть.

Принято считать, что работоспособные мелкие модели создать труднее. Но бывает и наоборот: более крупная приманка тоже нередко отказывается играть, и тогда, чтобы заставить ее работать, иногда приходится долго подбирать огрузку, размер и массу тройников, размер и форму лопасти и т. д. И не надо бояться экспериментировать. Скажем, мой хороший знакомый из Харькова предложил мне, одно время чрезмерно увлекавшемуся увеличением глубины хода, гнуть лопасти на продуктах неудачных экспериментов. Пользуясь этим методом, мне удалось запустить немало неработающих моделей (фото 3) Хотя в случае плексигласовой лопасти здесь не обойтись без дополнительной термообработки.

А вообще скажу: как правило, любую модель удается заставить сносно играть, если повозиться с ней как следует. И поверьте мне, игра стоит свеч. Особенно приятно, когда на рыбалке срабатывает не заведомо удачная приманка, сделанная по отработанной методике, а именно плод ваших долгих мучений. И тогда с гордостью говоришь себе: не зря я возился!

Ну, а в заключение хотелось бы еще раз извиниться перед теми из читателей, чье видение причин игры воблеров отличается от моего. Повторяю, я не специалист. Я просто изложил здесь свои представления, потому что, насколько мне известно, никто из экспертов до сих пор не опубликовал сколько-нибудь развернутого объяснения причин колебаний воблера, по крайней мере, в популярной литературе. Да это, возможно, им и не нужно, учитывая современный уровень развития кибернетики. В настоящее время существует ряд программ, позволяющих напрямую просчитать поведение тела в потоке жидкости или газа, задав только параметры тела и среды и даже не вникая в суть расчетов. А что же делать тем, для кого воблер - увлечение, а не объект профессионального внимания? Я надеюсь, кому-нибудь мои рассуждения будут интересны. Ну, а тех, кто собирается критиковать их, прошу писать мне на адрес редакции. А еще лучше - изложите свои представления на бумаге и опубликуйте их. В споре рождается истина. Банально, но факт.

Автор выражает искреннюю благодарность доктору физ.-мат. наук, профессору Олегу Лимарченко за бесценные консультации и плодотворные дискуссии.

Автор: Александр Даценко